Binary Search

Binary search is one of the more well-known algorithms, and probably the first formal algorithm someone is introduced to. I certainly had an “aha!” moment after learning how it functions and how it compares to doing a simple search via iteration.

The fundamental idea behind the algorithm is considering a sorted list of items and searching for a particular item, keep halving the list until the item is found or the the sublist is empty.

It has a worst-case time complexity of O(lg n), which is generally the case with algorithms that reduce their total items in half per step. So given n items, binary search takes n / 2^k steps: n -> n/2 -> n/4...1

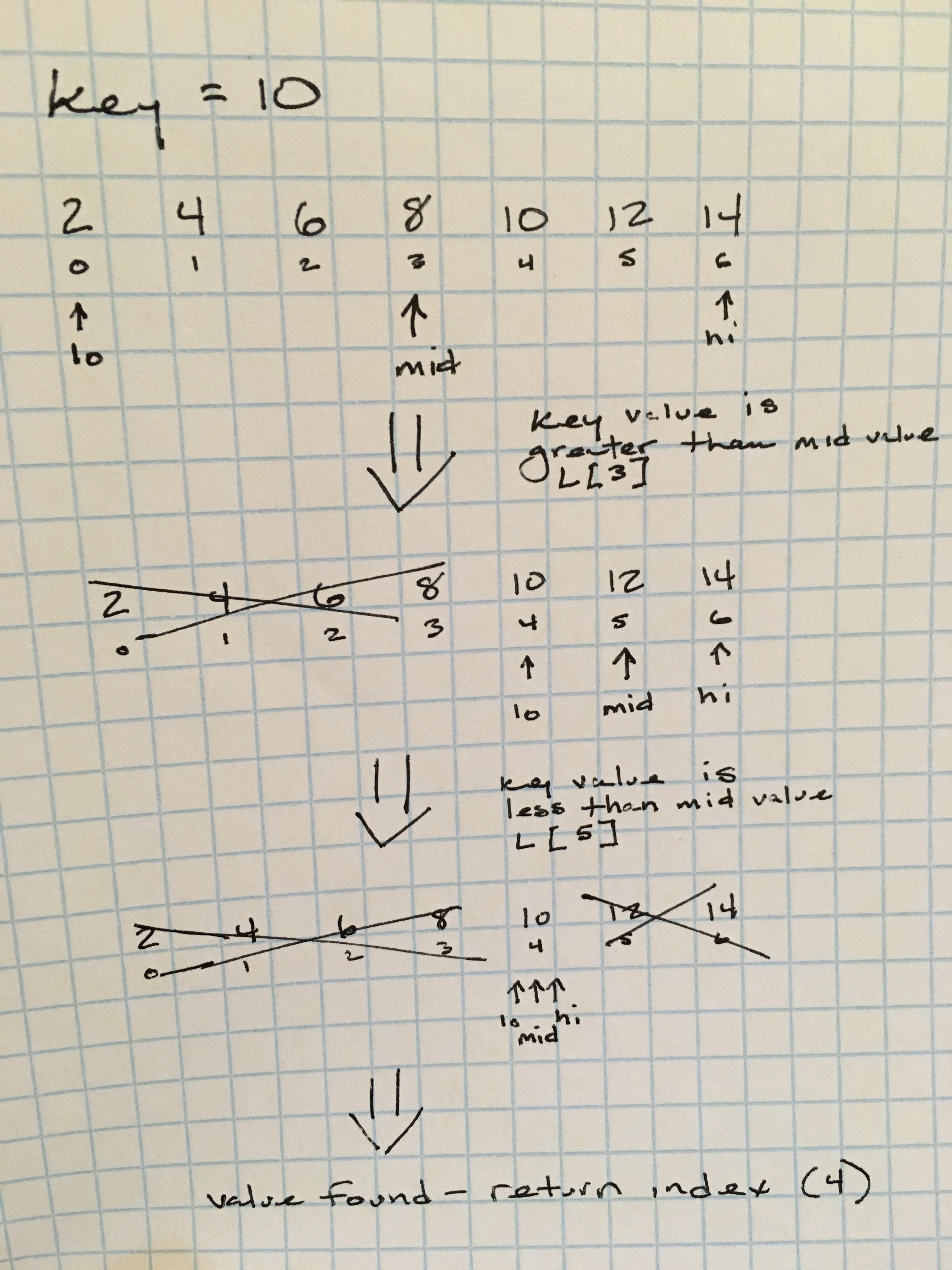
I’m adding example code here in Python instead of Java because Python really lets you see how the algorithm works when a type system can be set aside. The recursive implementation:

def search(L, lo, hi, key):
    if lo > hi: return -1

    mid = (lo + hi) / 2

    if L[mid] < key:
        # seach left of mid
        return search(L, mid + 1, hi, key)
    elif L[mid] > key:
        # search right of mid
        return search(L, lo, mid - 1, key)
    else:
        return mid

And the iterative implementation:

def search(L, lo, hi, key):
    while lo <= hi:
        mid = (lo + hi) / 2

        if L[mid] < key:
            hi = mid - 1
        elif L[mid] > key:
            lo = mid + 1
        else:
            return mid
    return -1