I found it helpful to wrangle some terminology around trees, binary trees, and binary heaps. Let’s start with trees…
Tree Basics
A tree is an efficient way to store and organize data in a naturally hierarchical way.
This data structure is comprised of nodes and edges.
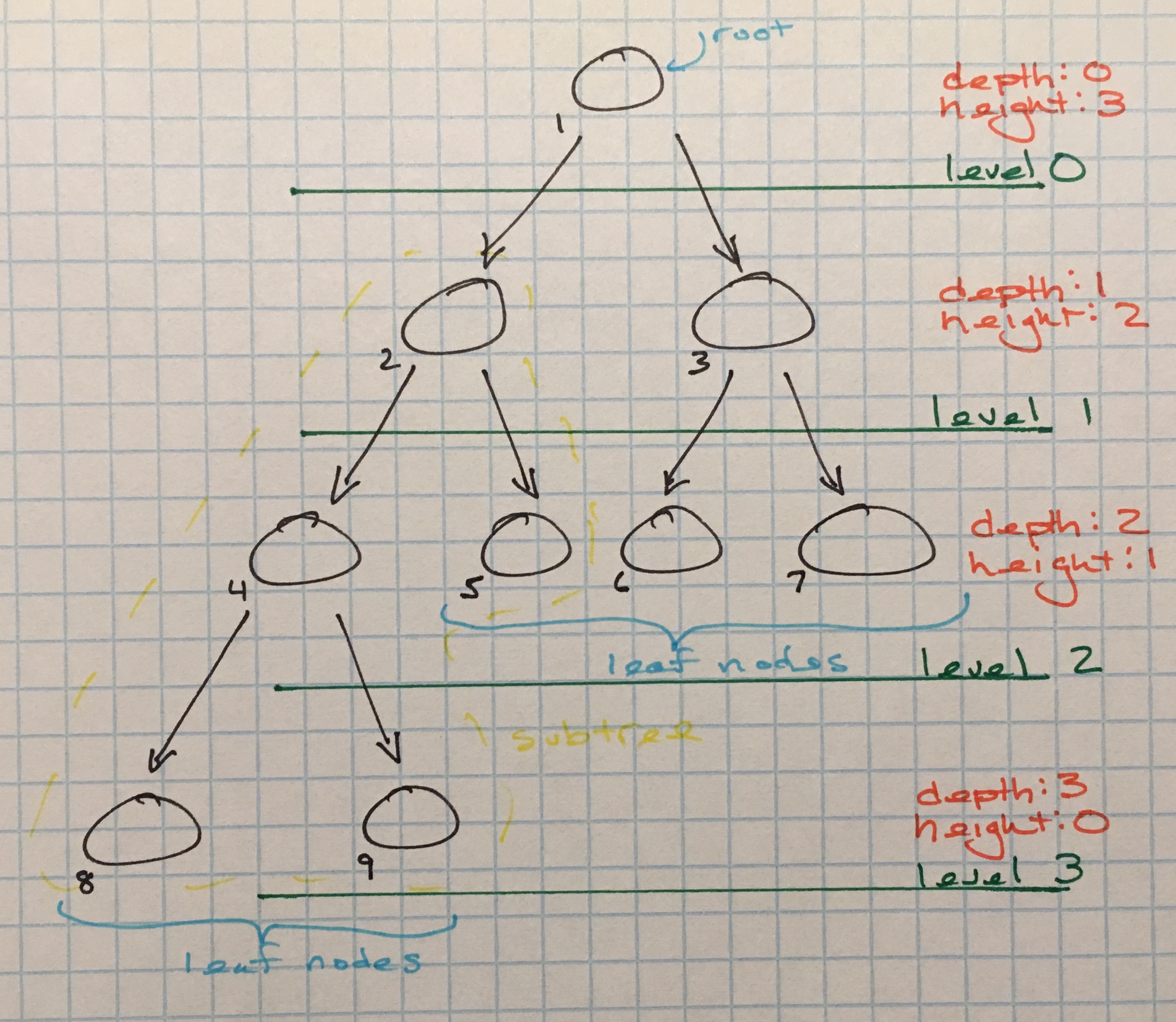
A node contains data and may or may not have a reference to a child node. Nodes without at least one child are leaf nodes; nodes with at least one child are called internal nodes or parent nodes. The highest node in the tree is the root node.
Edges are the connections between nodes.
Walking a tree is directional; the walk follows edges from the root node to the leaf nodes.
It is a recursive data structure and any tree can have subtrees, which are simply smaller segments of a tree inside the larger tree.
A tree with n nodes will always have n-1 edges and all nodes have incoming edges, with the exception of the root.
Given node k, the height of the node is the number of edges in the longest path from k to a leaf node. The depth of the node is the number of edges from the root node to node k.
Furthermore, the height of a tree is the number of edges from the root to the lowest leaf. It should be noted that a tree with one node is height 0 (so a tree with zero nodes is height -1).
Binary Trees
The binary tree is a tree where each node has at most two children.
The are a handful of ways to describle characteristics of binary trees:
- complete binary tree:
- all levels except possibly the last level are completely filled
- all nodes are left-directed (as far left as possible)
- the height of a complete binary tree is ⌊log n⌋
- perfect binary tree:
- the same idea as a complete binary tree, except all levels are completely filled
- total number of nodes equals 2ⁿ-1, n equaling the number of levels in the tree
- balanced binary tree:
- the difference between the height of the left subtree and right subtree for every node is not more x (x typically being 1)
- the difference is calculated as |heightleft_subtree - heightright_subtree|
Binary trees can be stored dynamically using pointers or in an array. However, using an array is only true for complete binary trees. Because I was planning on writing about binary heaps, I will leave dynamically creating a binary tree to a later post.
Binary Heaps and Priority Queues
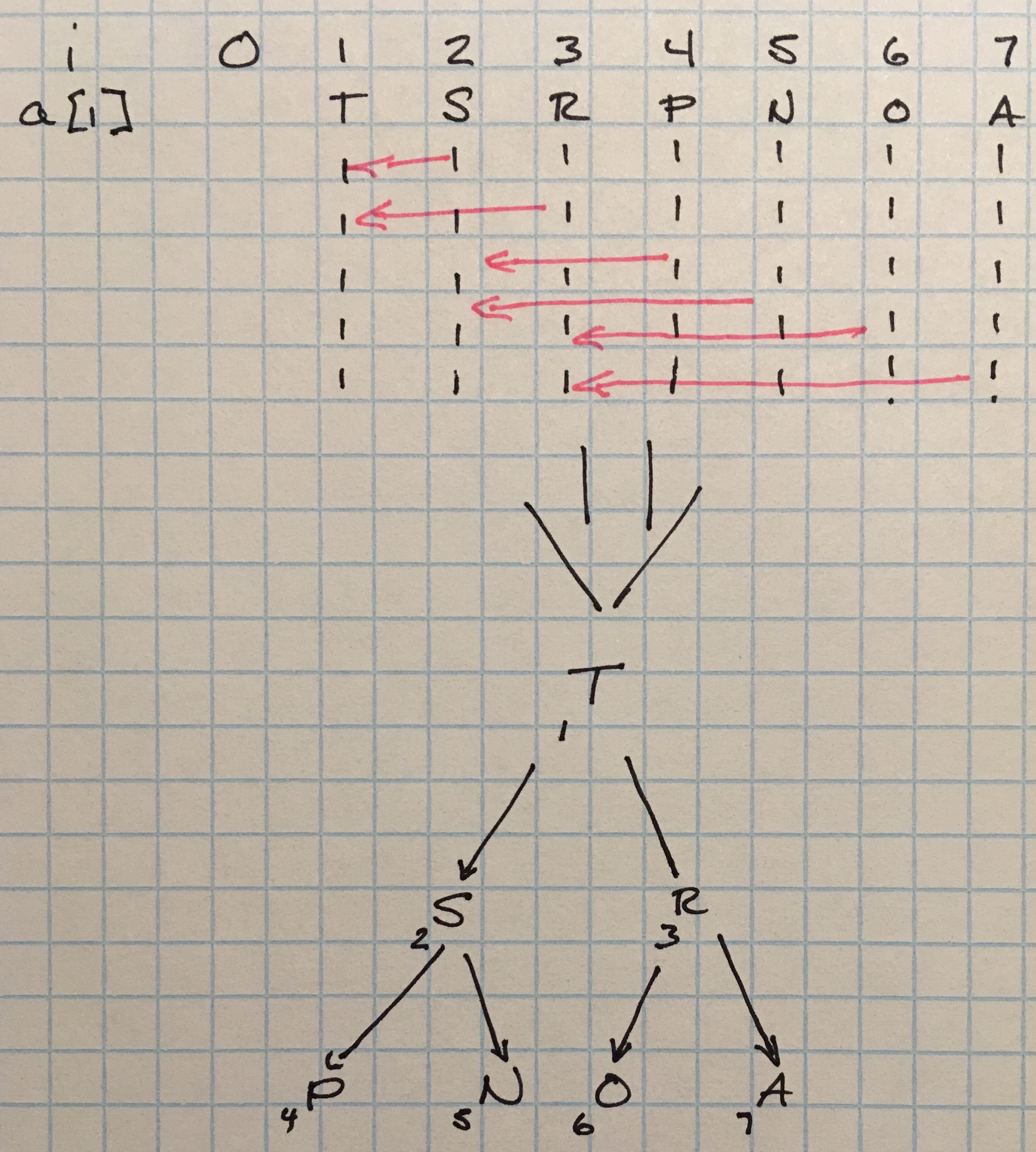
A binary heap is an array representation of a heap-ordered, complete binary tree. The level ordered of the the complete binary tree map to indices in the array.
What does heap ordered mean? Depending on whether the order of keys in the binary tree is ascending or descending, it means:
- the node’s data value is greater than or equal to the data value of its parent, the minimum value at the data value of the root node (this is min-heap), or:
- the node’s data value is lesser than or equal to the data value of its parent, with max value at the data value of the root node ( this is known as max-heap)
The binary heap is not a sorted data structure, but can be regarded as partially sorted; the heap will always keep the minimum value (or max value) as the first item in the array.
The heap is an excellent data structure for a priority queue (PQ) ADT. Priority queues are characterized by removing the smallest item (or largest depending on heap order) of a collection.
A typical example for the use of a PQ is given a stream of n items, find the largest m items. While sorting is the traditional way to solve this problem, PQs are handy when there is not enough memory to store all items for a sort.
Priority Queue Implementation
A typical PQ API will have the following methods. Note: I will be using a max-heap ordered binary heap for this example.
public class MaxPQ<Key extends Comparable<Key>>
MaxPQ() // create an empty PQ
MaxPQ(Key[] a) // create a PQ with given keys
void insert(Key v) // insert a key into the PQ
Key delMax() // return and remove the largest key
boolean isEmpty() // is the PQ empty?
Key max() // return the largest key
int size() // number of entries in the PQ
The binary heap starts at the 1-index position of the array for simplifying arithmetic operations used to update the PQ.
PQ - Basic Operations
When a child node in the heap becomes a larger key than its parent key, it needs to be swapped with the parent. This process continues until heap order is restored. The method responsible for this work is swim().
Insertions into the PQ are added to the end of the array, and swim() is then called to move the new node up the tree, if needed.
Conversely, when a parent becomes smaller than one or both of its children (after removing the max item from the heap), the sink() operation is called on that parent. This is accomplished by swapping the parent node with the largest of the children. This process continues until the violation is corrected.
delMax() removes and returns the maximum value in the binary heap by caching the value in 1-index position, swapping it with the last item in the heap, then sinking the item put in 1-index position until order is restored.
Below is a simplified version of how a PQ works. Array resizing and iteration code were omitted to focus the main concepts of how a PQ works.
public class MaxPQ<Key extends Comparable<Key>> {
private Key[] pq;
private int N; // total entries in the PQ
public MaxPQ(int capacity) {
// cast to `Key[]` - Java does not allow generic arrays
pq = (Key[]) new Comparable[capacity + 1];
}
public boolean isEmpty() { return N == 0; }
public void insert(Key key) {
pq[++N] = key; // add item to last position
swim(N); // restore order
}
public Key max() {
if (isEmpty()) throw new NoSuchElementException("Priority queue underflow");
return pq[1];
}
public Key delMax() {
key max = pq[1]; // cache max key (first item in array)
exch(1, N--); // exchange with last item
pq[N+1] = null; // prevent loitering (+1 because 1-based index)
sink(1); // restore heap order
return max;
}
private void swim(int k) {
// parent of `k` is k/2`
// while the parent of k is less than k, promote k
while (k > 1 && less(k/2, k)) {
exch(k/2, k);
k = k/2;
}
}
private void sink(int k) {
// child nodes are `2*k` and `2*k+1`
// determine largest child; exchange parent with largest child
while (2*k <= N) {
int j = 2*k;
if (j < N && less(j, j+1)) j++;
if (!less(k, j)) break;
k = j;
}
}
// helper methods
private boolean less(int i, int j) {
return pq[i].compareTo(pq[j]) < 0;
}
private void exch(int i, int j) {
Key temp = pq[i];
pq[i] = pq[j];
pq[j] = temp;
}
}
In regards to performance, insert() and delMax() are guaranteed to perform in O(log n) time. max() performs in O(1) time.