Binary search trees are a special type of binary tree where nodes are in symmetric order; for each node:
- the values of all nodes in the left subtree are lesser or equal
- and values of all nodes in the right subtree are greater
BSTs are excellent for modifiable collections with search and insertion operations. Basic operation are on average performed in O(log n) time, and in worst case O(n). The running time of operations on a BST are determined by the tree shape. In order for the best case running time, the keys need to be inserted in random order. In the worst case, they are inserted in order or reverse-order, which means the tree is shaped like a linked-list.
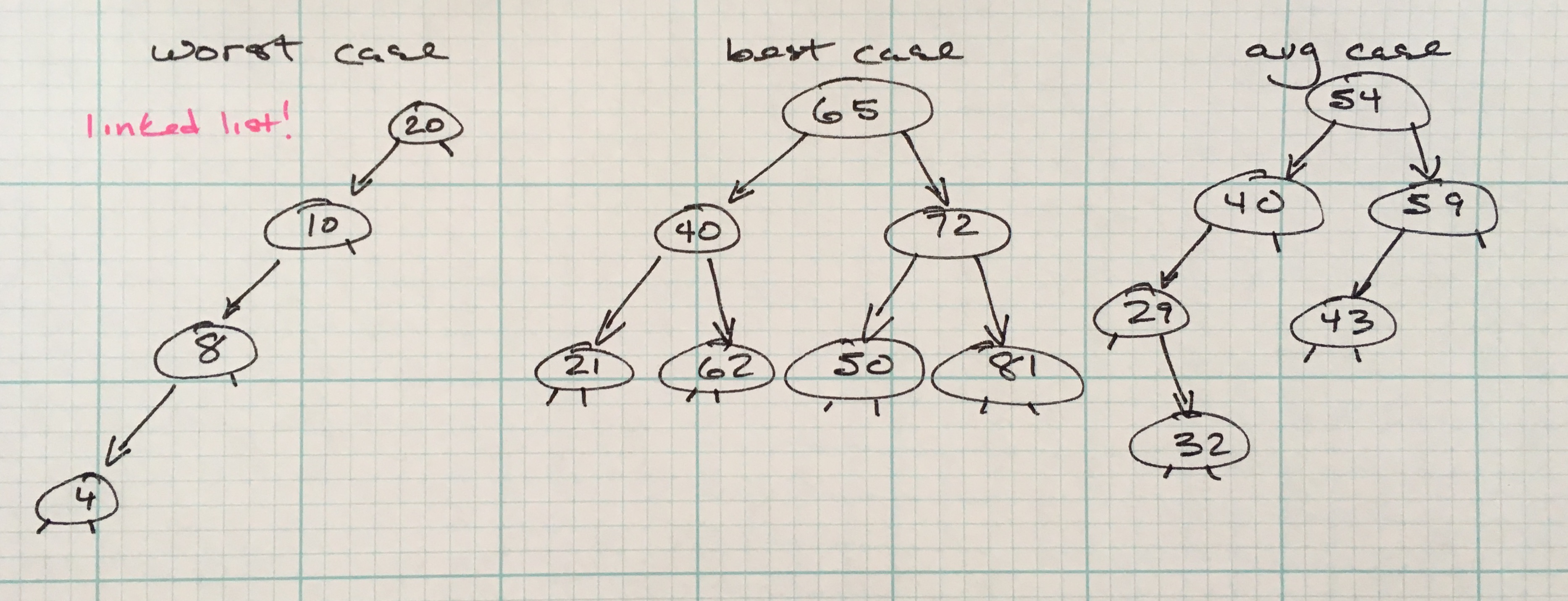
In my previous post, an array was used to represent a binary tree. The example in this post will use dynamic references to keep track of nodes and their children to represent the tree.
public class BST<Value extends Comparable<Value>> {
// root of BST instance
private Node root;
private class Node {
private Value val;
// links to subtrees
private Node left, right;
// nodes in subtree rooted here
private int N;
public Node(Value val, int N) {
this.val = val;
this.N = N;
}
}
public int size() { return size(root); }
private int size(Node x) {
if (x == null) return 0;
else return x.N;
}
public boolean search(Value val) {
if (search(root, val).equals(null)) return false;
return true;
}
private Value search(Node x, Value val) {
if (x == null) return null;
int cmp = val.compareTo(x.val);
if (cmp < 0) return search(x.left, val);
else if (cmp > 0) return search(x.right, val);
else return x.val;
}
public void put(Value val) {
root = put(root, val);
}
private Node put(Node x, Value val) {
if (x == null) return new Node(val , 1);
int cmp = val.compareTo(x.val);
// recursively call `put` on the left or right subtree
if (cmp < 0) x.left = put(x.left, val);
else if (cmp > 0) x.right = put(x.right, val);
// otherwise update the current value
else x.val = val;
// records the size of subtree for each node, for public `size` method
x.N = size(x.left) + size(x.right) + 1;
return x;
}
}
Traversing the BST
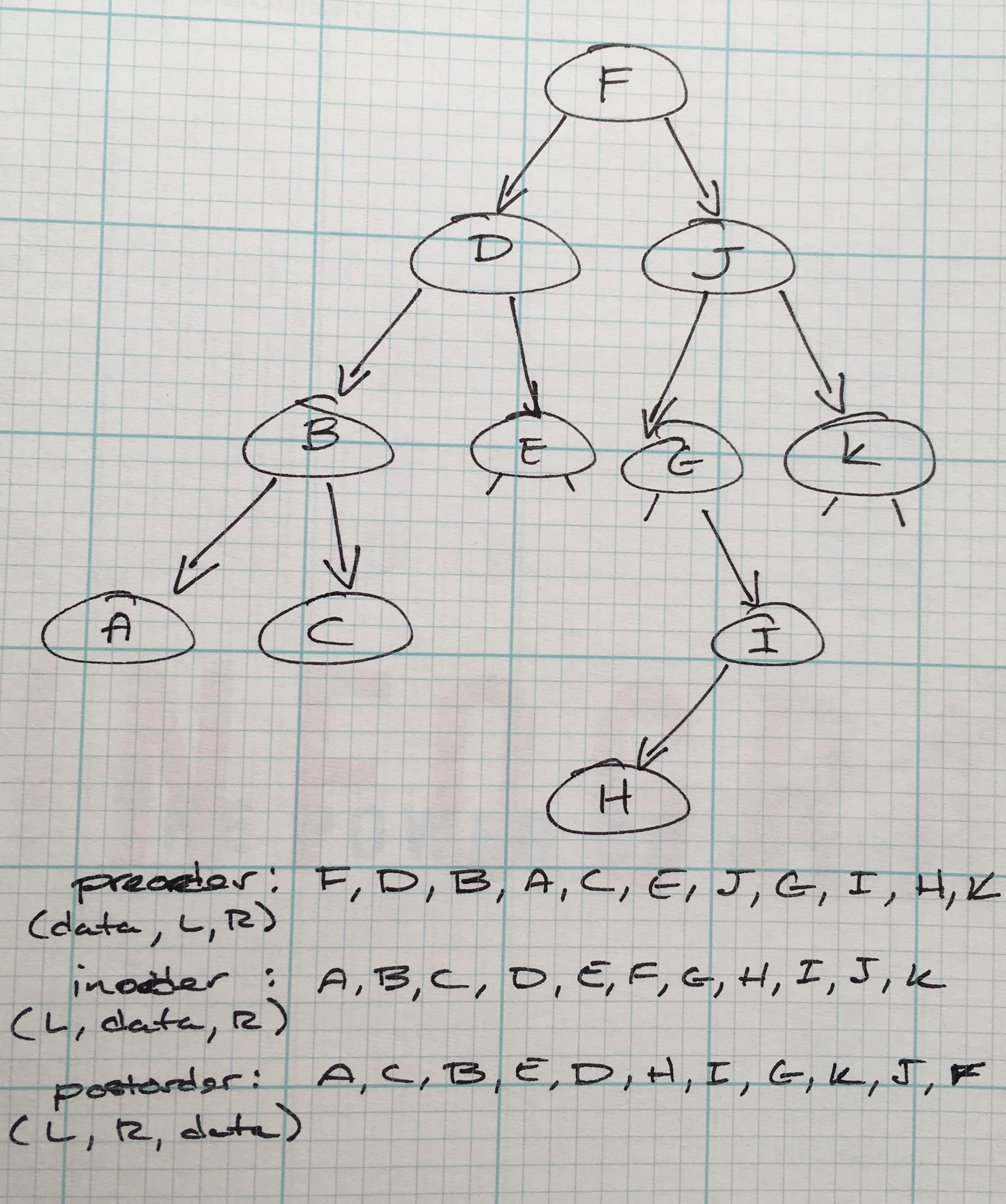
There are multiple orders to traverse a BST, and can be broken down into two main differentiations:
Depth-First Traversal
The depth-first strategy means the visiting path for a child node will visit the node’s subtree.
The order can be relative:
- preorder:
<root><left><right> - inorder:
<left><root><right> - postorder:
<left><right><root>
An inorder traversal of a BST will print a sorted list!
public void inorder(Node x) {
if (x == null) return;
inorder(x.left);
System.out.println(x.val) ;
inorder(x.right);
}
Logging in preorder or postorder is simply a matter of re-ordering the recursive method calls and println().
It should be noted the space complexity for depth first is O(h), h equaling the height of the tree, as recursive call stack frames are added and removed from the call stack. The call stack will grow until a leaf node is reached, at which it starts to shrink.
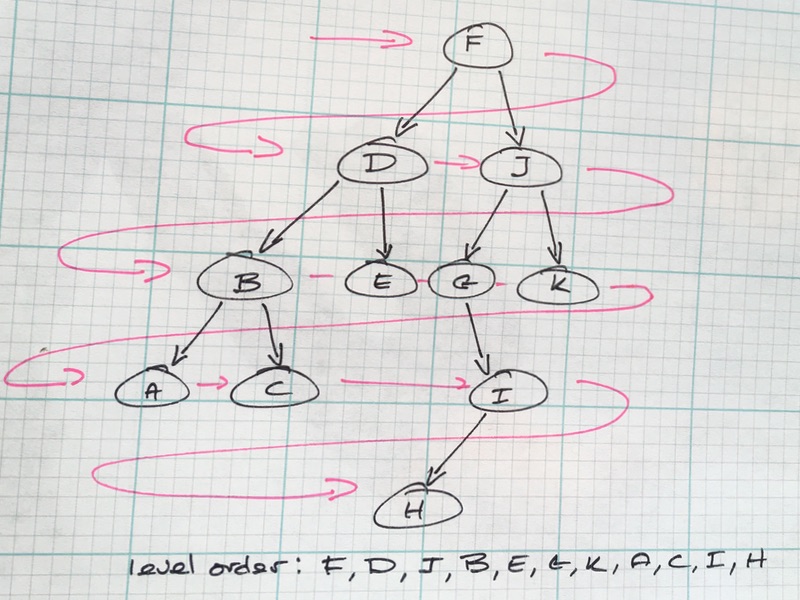
Breadth-First Traversal
A breadth-first traversal of a BST is visiting nodes in level order, from left to right. It uses a queue data structure to store references to the nodes, so the oldest node added is the next node value removed and printed, then.
public void levelOrder() {
if (root == null) return;
Queue q<Node> = new Queue<>();
q.enqueue(root);
while (!q.isEmpty()) {
Node x = q.dequeue();
System.out.println(x.val);
if (x.left != null) q.enqueue(x.left);
if (x.right != null) q.enqueue(x.right);
q.dequeue();
}
}
Because every node in the tree is being read in a traversal, the running time is O(n) no matter the tree shape. The queue used means the space complexity is O(n) as well.
These traversal strategies can also be used for binary trees. The only difference between a BST and binary tree is the inorder strategy will not print the items in their natural order for binary trees.
Keeping BSTs balanced
As noted above, in order to keep the O(log n) time complexity, tree shape needs to be balanced. As inserts and deletions are performed, BSTs degrade in performance as subtrees become longer than others. There are solutions for this problem, specifically 2-3 trees and Red-Black trees, which self-balance their subtrees. I hope to write more about this in a future post.