Hashmaps are a quintessential data structure; they are used everywhere. I wanted to write some notes on the underlying implementation for future reference.
Hashmaps (hash tables, associative arrays, dictionaries - they all mean the same thing) require:
- a hash function
- a hash collision resolution
Implementation
Hashmaps are used for quick look ups - for key k retrieve value v.
Under the hood, a hashmap stores values in an array, using an index to look up the value associated with a key. This is where the hash function comes into play - given a key (typically a string), hash the string to provide an index to store the associated value.
Hash(K) -> index
A good hash function, given a data type:
- is consistent; equal keys provide the same hash value.
- is efficient.
- uniformly distributes the set of keys between 0 and M-1, M being the array length.
It’s generally assumed getting and setting in a hashmap is O(1) (amortized time) if the hashing function is performant. However, in reality this isn’t always the case.
Resizing
Collision Resolution
Collisions will happen; keys can have different hashes but end up with the same index. There are infinitely more key possibilities than there are indices in the array.
Collision resolution is the strategy for handling when two or more keys hash to the same index. Seperate chaining and linear probing are the more common strategies.
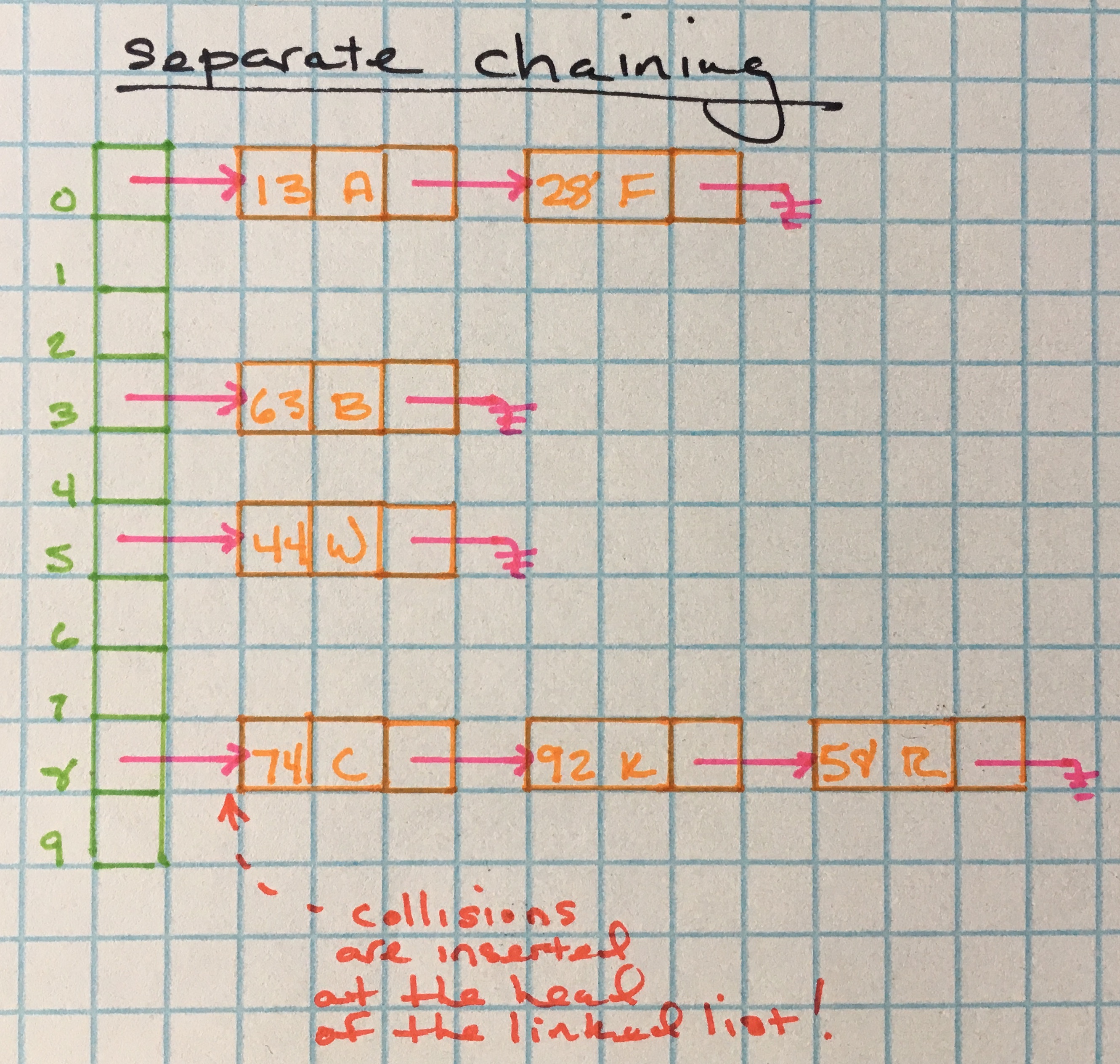
Seperate Chaining
This is the most common collision resolution in the wild. Instead of storing values directly in an array index, each array index stores a linked list, where the k:v pair is added to a new linked list node, and inserted into the linked list.
Essentially, items with key hashes that collide are chained together in linked lists.
public class HashMapSC<K, V> {
private class Node<K, V> {
K key;
V val;
Node<K, V> next;
public Node(K key, V val) {
this.key = key;
this.val = val;
}
}
private Node[] table;
// size of table
private int capacity;
// total items in hashmap
private int size;
public HashMapSC() { this(997); }
public HashMapSC(int capacity) {
this.capacity = capacity;
table = new Node[capacity];
size = 0;
}
public int size() { return size; }
public boolean isEmpty() { return size == 0; }
public void put(K key, V val) {
if (key == null || val == null) throw new IllegalArgumentException();
// double table capacity if necessary
if (size >= capacity / 2) resize(capacity * 2);
int index = hash(key);
Node nextNode = new Node(key, val);
Node curr = table[index];
// insert new node at head of linked list
if (curr == null) {
nextNode.next = curr;
table[index] = nextNode;
size++;
return;
}
// if linked list has nodes, replace val if key in list
while (curr != null) {
if (curr.key.equals(key)) {
// replace update val
curr.val = val;
}
curr = curr.next;
}
}
public V get(K key) {
if (key == null) throw new IllegalArgumentException();
int index = hash(key);
Node node = table[index];
while (node != null) {
if (node.key.equals(key)) return (V) node.val;
node = node.next;
}
return null;
}
private K remove(K key) {
if (key == null) throw new IllegalArgumentException();
int index = hash(key);
Node curr = table[index];
Node prev = null;
while (curr != null) {
if (curr.key.equals(key)) {
size--;
// halve the table capacity if necessary
if (size > 0 && size < (capacity / 8)) resize(capacity / 2);
if (prev == null) {
// removing first item in linked list
table[index] = curr.next;
} else {
prev.next = curr.next;
table[index] = prev;
}
return key;
}
prev = curr;
curr = curr.next;
}
return null;
}
private int hash(K key) {
return (key.hashCode() & 0x7fffffff) % capacity;
}
private void resize(int size) {
Node[] copy = new Node[size];
for (int i = 0; i < size; i++) {
copy[i] = table[i];
}
table = copy;
}
public static void main(String[] args) {
HashMapSC hm = new HashMapSC<String, Integer>();
hm.put("homer", 123);
hm.put("marge", 456);
assert hm.size() == 2;
assert hm.get("homer").equals(123);
assert hm.get("marge").equals(456);
hm.put("marge", 654);
assert hm.get("marge").equals(654);
assert hm.remove("marge").equals("marge");
assert hm.size() == 1;
}
}
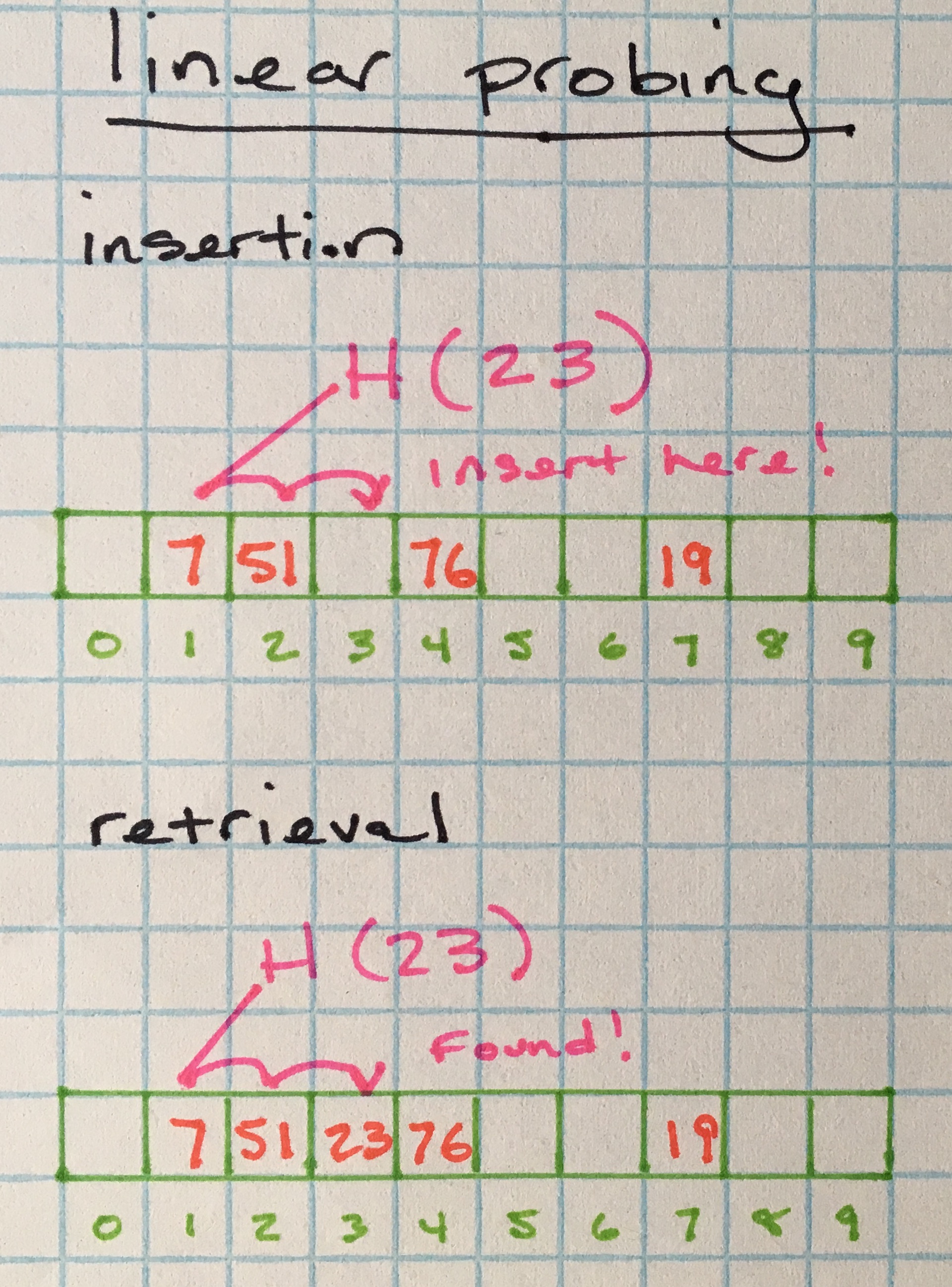
Linear Probing
Another common method for collision resolution is linear probing.
While seperate chaining uses linked lists at indices to resolve collisions, a linear probing strategy stores the values (or references to values) in the buckets. When the hash function hashes to a table index that’s already occupied, it probes for the next empty position in the array (by incrementing a pointer).
Retrieval works similarly; if the hash function hashes to an index that does not match the given key, the index increments by 1 and checks again. This is repeated until there’s a key match. Otherwise null is returned.
Parallel arrays, one for keys and one for values.
public class HashMapLP<K, V> {
private int size;
private int capacity;
private K[]keys;
private V[]vals;
public HashMapLP() {
this(4);
}
public HashMapLP(int capacity) {
this.capacity = capacity;
keys = (K[]) new Object[capacity];
vals = (V[]) new Object[capacity];
}
public int size() { return size; }
public boolean isEmpty() { return size == 0; }
public void put(K key, V val) {
if (key == null || val == null) throw new IllegalArgumentException();
// double the size of the table when it's at half capacity
if (size >= capacity / 2) resize(capacity * 2);
int i = hash(key);
// replace existing val
while(keys[i] != null) {
if(keys[i].equals(key)){
vals[i] = val;
return;
}
i = (i + 1) % capacity;
}
// insert new k:v pair
keys[i] = key;
vals[i] = val;
size++;
}
public V get(K key) {
if (key == null) throw new IllegalArgumentException();
int i = hash(key);
while (keys[i] != null) {
if (keys[i].equals(key)) return vals[i];
i = (i+1) % capacity;
}
return null;
}
public K remove(K key) {
if (key == null) throw new IllegalArgumentException();
int i = hash(key);
while (keys[i] != null) {
if (keys[i].equals(key)) {
key = keys[i];
keys[i] = null;
vals[i] = null;
size--;
if (size > 0 && size <= (capacity / 8)) resize(capacity / 2);
return key;
}
i = (i + 1) % capacity;
}
return null;
}
private void resize(int capacity) {
K[] keysCopy = (K[]) new Object[capacity];
V[] valsCopy = (V[]) new Object[capacity];
for (int i = 0; i < this.capacity; i++) {
if (keys[i] != null) {
keysCopy[i] = keys[i];
valsCopy[i] = vals[i];
}
}
this.capacity = capacity;
keys = keysCopy;
vals = valsCopy;
}
private int hash(K key) {
return (key.hashCode() & 0x7fffffff) % capacity;
}
}
Hashing
private int hash(K key) {
return (key.hashCode() & 0x7fffffff) % capacity;
}
The above hashing algorithm is a simple in its design.
The hashing algorithm needs to ensure it does not provide a negative number. Without ensuring this, we know it’s a possibility because hashCode() can provide negative values
We can ensure a positive number is provided by performing a shift mask using bitwise ANDing; it extracts the common bits between the result of key.hashcode() and the hexadecimal value for 214,7483,647, which uncoincidentally is the max integer value a Java-32 bit integer can hold. The max value is used to take advantage of the largest number of bits possible. This value is divided by the array length and remainder, in principle, should represent an array index value that is of uniform distribution for all possible array index values.